期望最大化算法,是寻找具有潜在变量地概率模型地最大似然解的一种通用的方法。下面介绍一般形式的EM算法的推导过程。
| 我们把所有的观测变量联合起来记作$X={x_1, x_2, …, x_N}$,将所有的隐含变量记作$Z={z_1, z_2, x_N}$。这里只考虑$Z$的状态是离散值的情况,我们假设每个样本$x_n$点由对应的隐含变量$z_n$决定。于是对于生成式模型,我们希望模型的参数集$\theta$能够使得$p(X | \theta)$的概率达到最大。因此很容易想到最大化模型的似然函数就能解出最优的参数集$\theta$。 |
我们通过计算$(X,Z)$的联合概率密度分布计算$X$的边缘概率密度: 对上式使用极大似然法求解参数$\theta$的最优解过程中,需要对左右同时取对数,观察右边部分$ln \sum _Z p(X, Z|\theta)$,我们会发现对潜在变量的求和出现在了对数运算内部,这阻止了对数运算直接作用于联合概率分布,使得最大似然解的形式更加复杂。
问题的转化
| 后面的介绍中,我们称${X, Z}$为完整的数据集,并且我们称实际观测的数据集$X$为不完整的,完整数据集的对数似然函数为$ln \ p(X,Z | \theta)$,我们假定这个完整数据集的对数似然函数进行最大化是很容易的。 |
下面介绍将最大化$p(X|\theta)$的目标转化成最优化$p(X,Z|\theta)$的过程。我们引入一个定义在潜在变量上的分布$q(Z)$,对于任意的$q(Z)$,下面的分解式成立: 其中,我们定义了
证明公式(2)
利用概率的乘积规则$p(X,Z \theta)=p(Z X,\theta) \ p(X \theta)$,于是$ln\ (X,Z \theta) = ln \ p(Z X,\theta) + ln\ p(X \theta)$,然后代入$\mathcal{L}(q, \theta)$的表达式。这得到了两项,一项消去了$KL(q p)$,而另外一项给出了所需的对数似然函数$ln\ p(X \theta)$,其中我们用到了归一化的概率分布$q(Z)$的积分等于1的事实。
| 我们来观察公式(2),右边的两项都是关于变量$q(Z)$和模型参数集${\theta}$的的函数,右边的第二项表示的是KL散度$KL(q, \theta)$是$q(Z)$和后验概率分布$p(X,Z | \theta)$之间的$Kullback-Leibler$散度。我们知道$Kullback-Leibler$散度满足$KL(q, \theta) \ge 0$,当且仅当$q(Z) = p(Z | X, \theta)$时等号成立。因此从公式(2)中我们可以得到一个结论:$\mathcal{L} (q, \theta)$是$ln \ p(X | \theta)$的一个下界。因此,既然$ln \ p(X | \theta)$无法使用极大似然法得到一个解析解,那么只要找到一种方法让这个下界不断接近$ln \ p(X | \theta)$,就能找到使得似然函数$p(X | \theta)$最大化的参数集$\theta$。下面介绍这些方法中一个通用的方法:EM算法。 |
EM算法的实现过程
| EM算法是一个两阶段的迭代优化算法,用于寻找$ln \ p(X | \theta)$最大似然解$\theta ^{opt}$。转化公式(2)包含两个参数${q(Z), \theta}$,假设参数向量的当前值为$\theta ^{旧}$,EM算法分类两个步骤: |
-
E步骤:固定$\theta ^{旧}$,$q(Z)$分布被设置为当前参数值$\theta ^{旧}$下的后验概率分布$p(Z X, \theta ^{旧})$,(2)式中的第二项$KL(q p)= - \sum _Z q(Z) ln {\frac{p(Z X,\theta)}{q(Z)}}$的取值为0。因此$ln \ p(X \theta ^{旧}) = \mathcal{L}(q, \theta ^{旧}) $,这使得$\theta ^{旧}$固定的情况下,下界上移到对数似然函数值相同的位置。$\theta ^{旧}$在未达到最大似然解$\theta ^{opt}$之前,$ln \ p(X \theta ^{旧}) \le ln \ p(X \theta ^{opt})$,于是我们通过M步骤更新$\theta ^{旧}$为$\theta ^{新}$,使得$\theta ^{新}$不断地逼近$\theta ^{opt}$。

-
M步骤:保持E步骤中计算得到的$q(Z)=p(Z X, \theta ^{旧})$固定,使下界$\mathcal {L}(q, \theta)$关于$\theta$进行最大化,得到某个新值$\theta ^{新}$。这会使下界$\mathcal{L}$增大(除非达到了极大值),这会使得对应的对数似然函数$ln \ p (X \theta^{新})$增大。原因是当前潜在变量的分布$q(Z)$由旧的参数值确定并且保持了固定,因此它不会等于新的后验概率分布$p(Z X, \theta ^{新})$,从而KL散度不为0。于是对数似然函数的增加量大于下界的增加量(下界增加量+新的KL散度值)。

| M步骤我们推导了通过对下界$\mathcal{L}(q, \theta)$进行最大化,更新迭代得到的$\theta ^{新}$对应的对数似然函数$ln \ p(X | Z, \theta ^{新}) > ln \ p(X | Z, \theta ^{旧})$,我们只要将E步骤中旧的参数$\theta ^{旧}$用M步骤的$\theta ^{新}$代替,如此持续迭代,就能使参数$\theta $不断逼近最优解$\theta ^{opt}$。 |
最大化下界$\mathcal{L}(q, \theta)$
我们将注意力放在M步骤中$\mathcal{L}(q, \theta)$的最大化上,使用$q(Z)=p(Z|X, \theta ^{旧})$代入下界函数$\mathcal{L}(q, \theta)$得到: 其中,常数就是分布$q$的熵,与$\theta$无关。观察公式(4)可知,M步骤后下界的增大值实际上等于完整数据似然函数的期望,我们记作$\mathcal{Q}(\theta, \theta _{旧})$。最大化$\mathcal{L}(q, \theta)$又转化成了最大化$\mathcal{Q}(\theta, \theta ^{旧})$,至此我们就将最大化$p(X|\theta)$目标转化成了关于$p(X, Z|\theta)$的问题,这样做的好处是使得我们要优化的$\theta$只出现在对数运算内部,如果联合概率分布$p(X,Z|\theta)$由指数族分布的成员组成,或者其乘积组成,那么对数运算会抵消指数运算,大大简化了运算的复杂度,解决了原来无法得到$\theta$解析解的问题。
$\mathcal{Q}(\theta, \theta ^{旧})$的最大化
| 经过上文的推导,我们对问题进行了两次转化,第一次在M步骤中将最优化$ln \ p(X | \theta)$的目标转化成最优化下界$\mathcal{L}(q, \theta)$的问题,第二次转化是将最优化下界$\mathcal{L}(q, \theta)$的目标转化成最优化$\mathcal{Q}(\theta, \theta _{旧})$的目标。 |
我们来讨论独立同分布数据集的情况,$X$由$N$个数据点${x_n}$组成,而$Z$由对应的N个潜在变量${z_n}$组成,其中$n={1,2,…,N}$。根据独立性假设,我们有$p(X, Z)= \prod _ n p(x_n, z_n)$,并通过关于${z_n}边缘概率分布,我们有 p(Z|X,\theta)=\frac {P(X, Z |\theta)}{\sum _Z p(X, Z|\theta)} =\frac{\prod _{n=1} ^{N} p(x_n, z_n|\theta)}{\sum _Z \prod _{n=1} ^{N} p(x_n, z_n|\theta)} =\prod _{n=1}^{N}p(z_n|x_n, \theta) $$ 因此后验概率分布也可以关于$n$进行分解。在高斯混合模型中,这个结果意味着混合分布的每个分量对于一个特定的数据点$x_n$的”责任“只与$x_n$的值和混合分量的参数$\theta$有关,而与其他数据点无关。
从参数空间角度理解EM算法
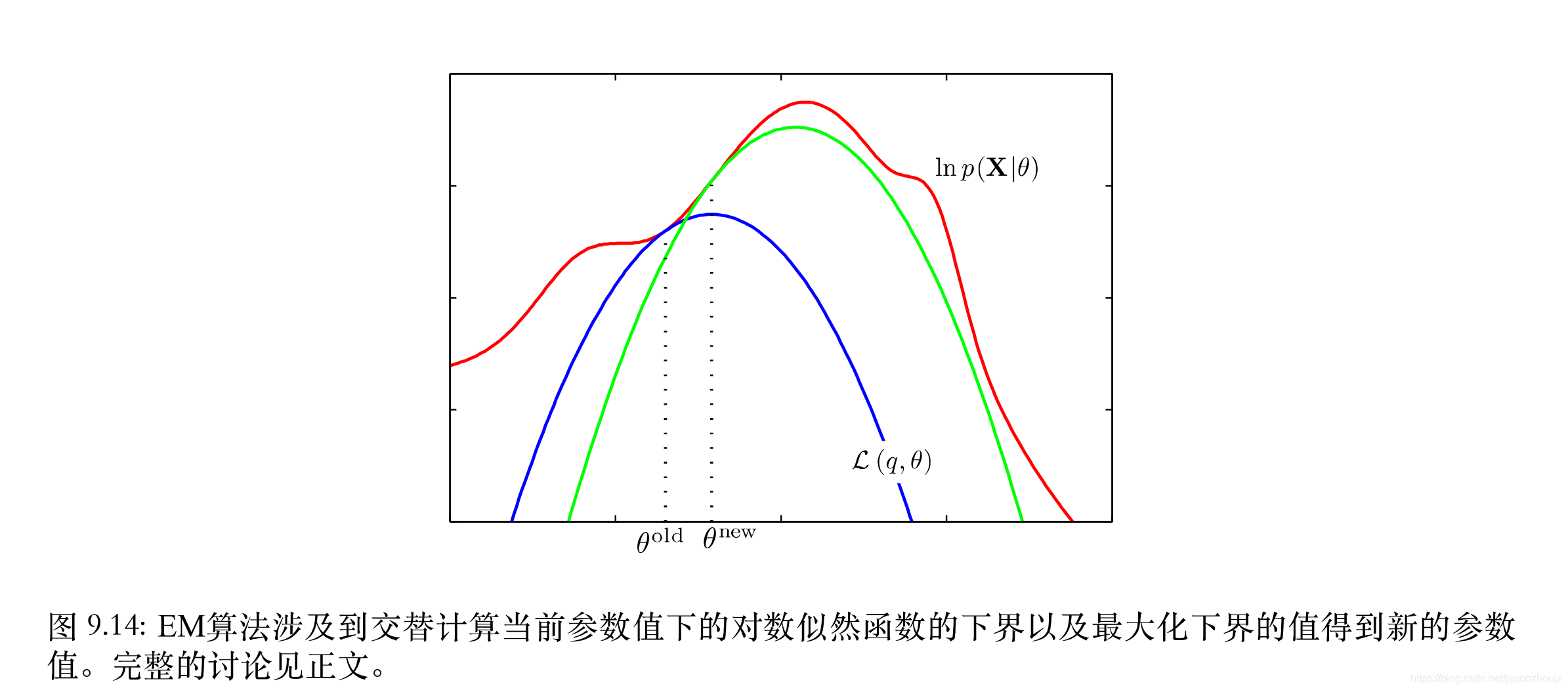
| 如上图所示,红色曲线表示(不完整数据)的对数似然函数,它的最大值是我们想要的。我们首先选择某一个初始的参数$\theta ^{旧}$,然后第一个E步骤中,我们计算潜在变量上的后验概率分布$p(Z | X, \theta ^{旧})$,我们使用$p(Z | X, \theta ^{旧})$代替$q(Z)$代入进而得到了一个较小的下界函数$\mathcal{L}(q, \theta ^{old})$,用蓝色曲线表示,下界和对数似然函数在$\theta ^{old}$处相切。并且这个下界函数$\mathcal{L}(q, \theta ^{old})$是一个凹函数,对于指数族分布的混合分布来说,有唯一的最大值,注意前面证明过下界函数$\mathcal{L}(q, \theta ^{old})$的最大值始终小于似然函数的最大值。因此在M步骤中,下界函数$\mathcal{L}(q, \theta)$被最大化,得到了新的参数$\theta ^{new}$,这个参数给出了比$\theta ^{old}$处更大的似然函数值。接下来的E步骤构建一个新的下界,它在$\theta ^{new}$处和似然函数相切,用绿色曲线表示。重复上面的步骤直到下界函数的最大值的增加率小于某个阈值。 |